Representative cycles

Note. This interface is a WIP, and is subject to change.

Invariant computations can be achieved via vineyard computation, which explicitely stores the representative cycles.

We show here how to recover them in python.

import multipers as mp
import matplotlib.pyplot as plt
import numpy as np
import gudhi as gd
import multipers.plots as mpp
np.random.seed(1)

[KeOps] Warning : CUDA libraries not found or could not be loaded; Switching to CPU only.

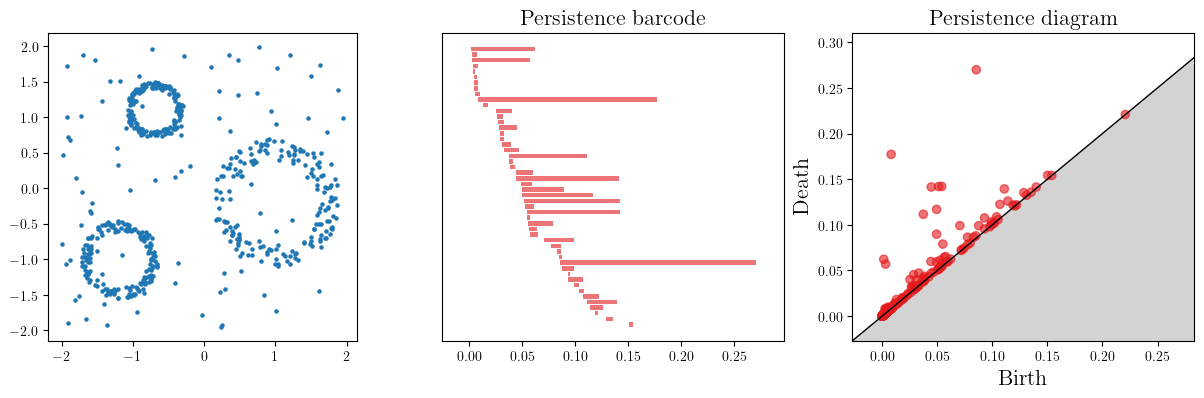
Usual noisy dataset.

np.random.seed(1)
X = mp.data.three_annulus(500, 100)
fig, (a,b,c) = plt.subplots(ncols=3, figsize=(15,4))
plt.sca(a)
plt.scatter(X[:,0], X[:,1], s=5); plt.gca().set_aspect(1)
st = gd.AlphaComplex(points=X).create_simplex_tree()
st.compute_persistence()
persistence=st.persistence_intervals_in_dimension(1)
gd.plot_persistence_barcode(persistence=persistence, axes=b, max_intervals=50)
gd.plot_persistence_diagram(persistence=persistence, axes=c)

/Users/dlapous/micromamba/envs/313/lib/python3.13/site-packages/gudhi/persistence_graphical_tools.py:107: UserWarning: There are 447 intervals given as input, whereas max_intervals is set to 50.
  warnings.warn(

<Axes: title={'center': 'Persistence diagram'}, xlabel='Birth', ylabel='Death'>

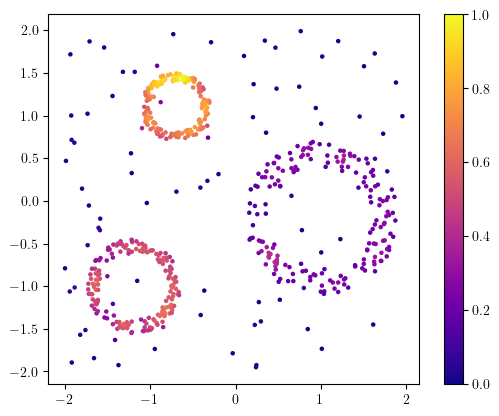
from multipers.filtrations.density import KDE
density = KDE(bandwidth=0.1).fit(X).score_samples(X)
# a bit of renormalization
density -= density.min()
density /= density.max()

plt.scatter(X[:,0], X[:,1], s=5, c=density, cmap="plasma")
plt.gca().set_aspect(1); plt.colorbar();

Let’s do a Rips codensity bifiltration

# as we already computed the density, we just need the RipsLowerstar filtration
from multipers.filtrations import RipsLowerstar
simplextree = RipsLowerstar(points=X, function = 1-density, threshold_radius=1.5) # this is a simplicial complex
simplextree.collapse_edges(-2)                             # Removes some unnecessary edges (while staying quasi isomorphic)
simplextree.expansion(2)                                   # Adds the 2-simplices (necessary for $H_1$ computations)

SimplexTreeMulti[dtype=float64,num_param=2,kcritical=False,is_squeezed=False,max_dim=2]

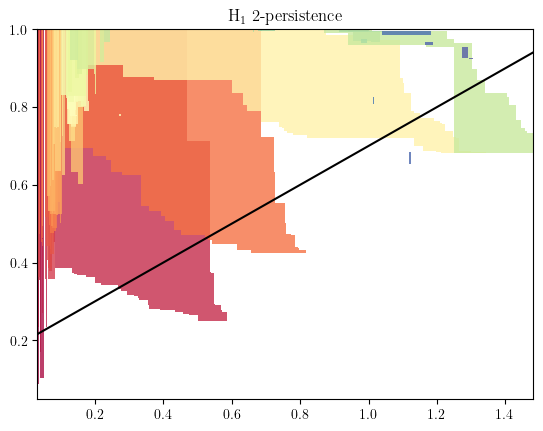
and compute an invariant

s = mp.Slicer(simplextree, vineyard=True) 

mod = mp.module_approximation(s.minpres(1))
mod.plot()
basepoint = np.array([.2,.3])
direction=np.array([2,1,])
slope=direction[1]/direction[0]
plt.axline(basepoint,slope=slope,c="k")

<matplotlib.lines.AxLine at 0x16bc08cd0>

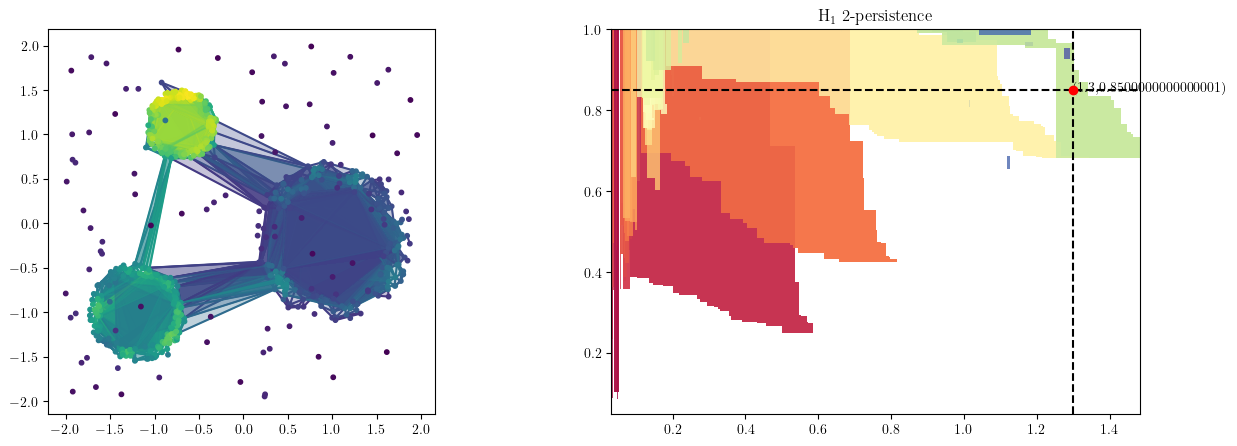
We draw the line that intersects the cycles we need to recover, and push s to it. This will fix the vineyard decomposition to this line filtration

s.push_to_line(basepoint=basepoint, direction=direction)

slicer[backend=Matrix,dtype=float64,num_param=2,vineyard=True,kcritical=False,is_squeezed=False,is_minpres=False,max_dim=2]

We can now compute the barcode of degree 1

bc = s.compute_persistence()[1]

And look at which cycles are nontrivial in this line slice

lifetimes = bc[:,1]-bc[:,0] 
idx = np.argwhere(lifetimes>0).ravel() # other criterion could be taken

We can then compute representative cycles of these cycles.

cycles = s.get_representative_cycles()[1] #
cycles = [cycles[i] for i in idx]

And plot them to double check it.

plt.scatter(*X.T, c=1-density, cmap="viridis_r")
plt.colorbar()

for cycle in cycles:
    cycle = np.array(cycle)
    B = X[cycle[:,0]]
    D = X[cycle[:,1]]
    # plt.scatter(X[:,0],X[:,1], c=density)
    for (a,b) in zip(B,D):
        plt.plot([a[0],b[0]],[a[1],b[1]], c="r")

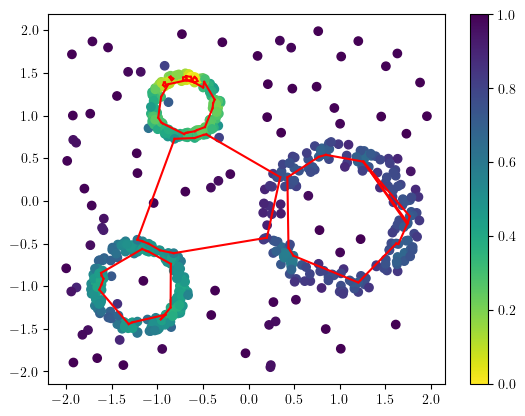
We can also double-check the cycles in the bifiltration.

from multipers.plots import plot_simplicial_complex
t = .55
radius, codens = basepoint + t *direction
plot_simplicial_complex(simplextree, X, radius, codens,mma=mod, degree=1)